Learn Statistics Estimating Population Proportions
A population proportion is the share of a population that belongs to a particular category.
Confidence intervals are used to estimate population proportions.
Estimating Population Proportions
A statistic from a sample is used to estimate a parameter of the population.
The most likely value for a parameter is the point estimate.
Additionally, we can calculate a lower bound and an upper bound for the estimated parameter.
The margin of error is the difference between the lower and upper bounds from the point estimate.
Together, the lower and upper bounds define a confidence interval.
Calculating a Confidence Interval
The following steps are used to calculate a confidence interval:
- Check the conditions
- Find the point estimate
- Decide the confidence level
- Calculate the margin of error
- Calculate the confidence interval
For example:
- Population: Nobel Prize winners
- Category: Born in the United States of America
We can take a sample and see how many of them were born in the US.
The sample data is used to make an estimation of the share of all the Nobel Prize winners born in the US.
By randomly selecting 30 Nobel Prize winners we could find that:
6 out of 30 Nobel Prize winners in the sample were born in the US
From this data we can calculate a confidence interval with the steps below.
Checking the Conditions
The conditions for calculating a confidence interval for a proportion are:
- The sample is randomly selected
- There is only two options:
- Being in the category
- Not being in the category
- The sample needs at least:
- 5 members in the category
- 5 members not in the category
In our example, we randomly selected 6 people that were born in the US.
The rest were not born in the US, so there are 24 in the other category.
The conditions are fulfilled in this case
Note: It is possible to calculate a confidence interval without having 5 of each category. But special adjustments need to be made.
Finding the Point Estimate

Deciding the Confidence Level
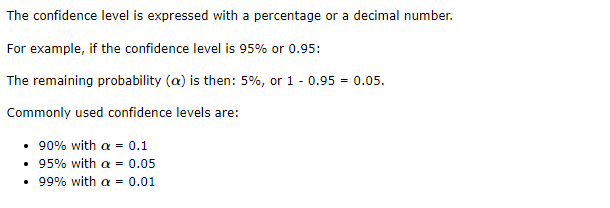
Note: A 95% confidence level means that if we take 100 different samples and make confidence intervals for each:
The true parameter will be inside the confidence interval 95 out of those 100 times.
We use the standard normal distribution to find the margin of error for the confidence interval.
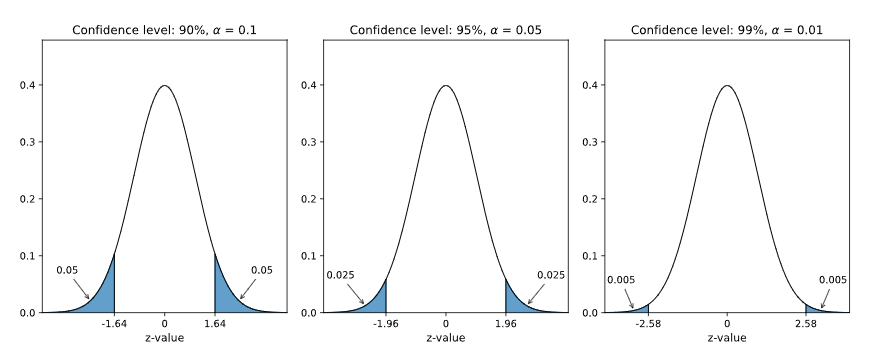
The remaining probabilities (α) are divided in two so that half is in each tail area of the distribution.
The values on the z-value axis that separate the tails area from the middle are called critical z-values.
Below are graphs of the standard normal distribution showing the tail areas (α) for different confidence levels.
Calculating the Margin of Error
The margin of error is the difference between the point estimate and the lower and upper bounds.
The margin of error (E) for a proportion is calculated with a critical z-value and the standard error:

Example
With Python use the Scipy Stats library norm.ppf() function find the Z-value for an
/2 = 0.025
import scipy.stats as stats
print(stats.norm.ppf(1-0.025))
Example
With R use the built-in qnorm() function to find the Z-value for an
/2 = 0.025
qnorm(1-0.025)
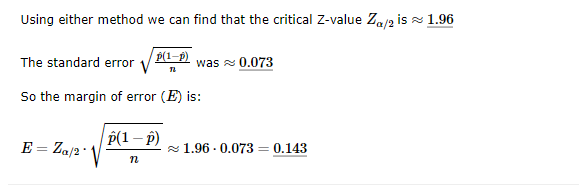
Calculate the Confidence Interval

The 95% confidence interval for the proportion of Nobel Prize winners born in the US is between 5.7% and 34.4%
Calculating a Confidence Interval with Programming
A confidence interval can be calculated with many programming languages.
Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.
Example
With Python, use the scipy and math libraries to calculate the confidence interval for an estimated proportion. Here, the sample size is 30 and the occurrences is 6.
import scipy.stats as stats
import math
# Specify sample occurrences (x), sample size (n) and confidence level
x = 6
n = 30
confidence_level = 0.95
# Calculate the point estimate, alpha, the critical z-value, the standard error, and the margin of error
point_estimate = x/n
alpha = (1-confidence_level)
critical_z = stats.norm.ppf(1-alpha/2)
standard_error = math.sqrt((point_estimate*(1-point_estimate)/n))
margin_of_error = critical_z * standard_error
# Calculate the lower and upper bound of the confidence interval
lower_bound = point_estimate - margin_of_error
upper_bound = point_estimate + margin_of_error
# Print the results
print("Point Estimate: {:.3f}".format(point_estimate))
print("Critical Z-value: {:.3f}".format(critical_z))
print("Margin of Error: {:.3f}".format(margin_of_error))
print("Confidence Interval: [{:.3f},{:.3f}]".format(lower_bound,upper_bound))
print("The {:.1%} confidence interval for the population proportion is:".format(confidence_level))
print("between {:.3f} and {:.3f}".format(lower_bound,upper_bound))
Example
With R, use the built-in math and statistics functions to calculate the confidence interval for an estimated proportion. Here, the sample size is 30 and the occurrences is 6.
# Specify sample occurrences (x), sample size (n) and confidence level
x = 6
n = 30
confidence_level = 0.95
# Calculate the point estimate, alpha, the critical z-value, the standard error, and the margin of error
point_estimate = x/n
alpha = (1-confidence_level)
critical_z = qnorm(1-alpha/2)
standard_error = sqrt(point_estimate*(1-point_estimate)/n)
margin_of_error = critical_z * standard_error
# Calculate the lower and upper bound of the confidence interval
lower_bound = point_estimate - margin_of_error
upper_bound = point_estimate + margin_of_error
# Print the results
sprintf("Point Estimate: %0.3f", point_estimate)
sprintf("Critical Z-value: %0.3f", critical_z)
sprintf("Margin of Error: %0.3f", margin_of_error)
sprintf("Confidence Interval: [%0.3f,%0.3f]", lower_bound, upper_bound)
sprintf("The %0.1f%% confidence interval for the population proportion is:", confidence_level*100)
sprintf("between %0.4f and %0.4f", lower_bound, upper_bound)