Learn Statistics Standard Normal Distribution
The standard normal distribution is a normal distribution where the mean is 0 and the standard deviation is 1.
Standard Normal Distribution
Normally distributed data can be transformed into a standard normal distribution.
Standardizing normally distributed data makes it easier to compare different sets of data.
The standard normal distribution is used for:
- Calculating confidence intervals
- Hypothesis tests
Here is a graph of the standard normal distribution with probability values (p-values) between the standard deviations:
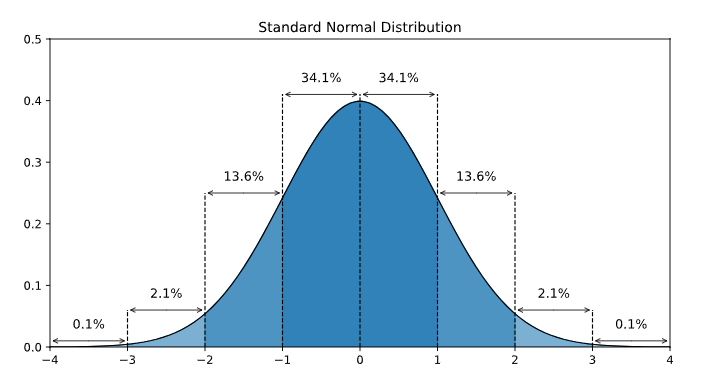
Standardizing makes it easier to calculate probabilities.
The functions for calculating probabilities are complex and difficult to calculate by hand.
Typically, probabilities are found by looking up tables of pre-calculated values, or by using software and programming.
The standard normal distribution is also called the 'Z-distribution' and the values are called 'Z-values' (or Z-scores).
Z-Values
Z-values express how many standard deviations from the mean a value is.
The formula for calculating a Z-value is:
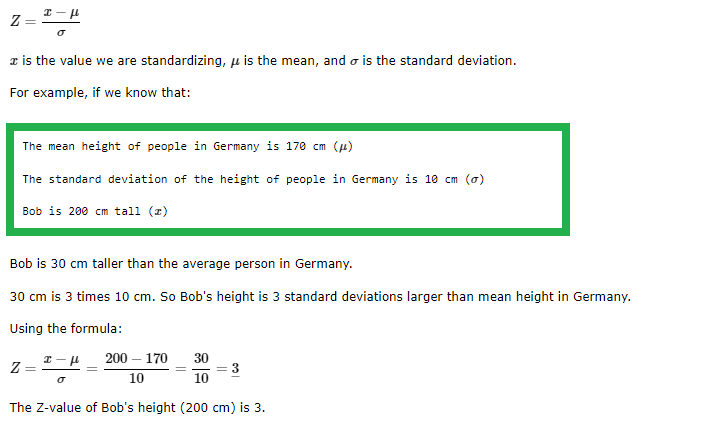
Finding the P-value of a Z-Value
Using a Z-table or programming we can calculate how many people Germany are shorter than Bob and how many are taller.
Example
With Python use the Scipy Stats library norm.cdf() function find the probability of getting less than a Z-value of 3:
import scipy.stats as stats
print(stats.norm.cdf(3))
Example
With R use the built-in pnorm() function find the probability of getting less than a Z-value of 3:
pnorm(3)
Using either method we can find that the probability is ≈ 0.9987, or 99.87% , or
Which means that Bob is taller than 99.87% of the people in Germany.
Here is a graph of the standard normal distribution and a Z-value of 3 to visualize the probability:
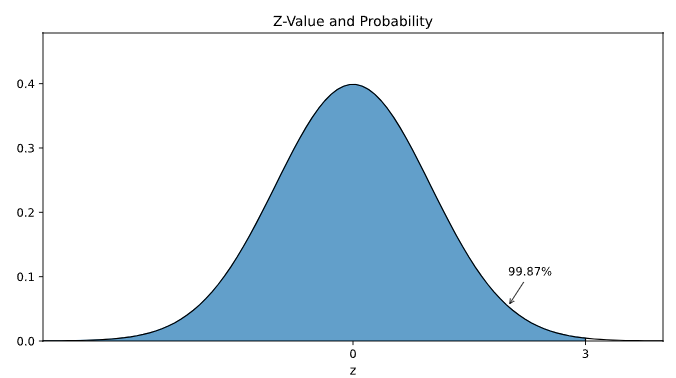
These methods find the p-value up to the particular z-value we have.
To find the p-value above the z-value we can calculate 1 minus the probability.
So in Bob's example, we can calculate 1 - 0.9987 = 0.0013, or 0.13%.
Which means that only 0.13% of Germans are taller than Bob.
Finding the P-Value Between Z-Values
If we instead want to know how many people are between 155 cm and 165 cm in Germany using the same example:
The mean height of people in Germany is 170 cm (𝜇)
The standard deviation of the height of people in Germany is 10 cm (𝜎)
Now we need to calculate Z-values for both 155 cm and 165 cm:
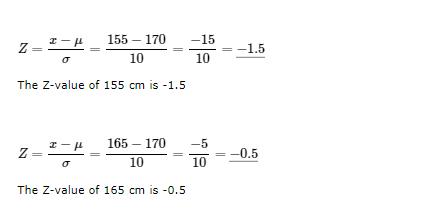
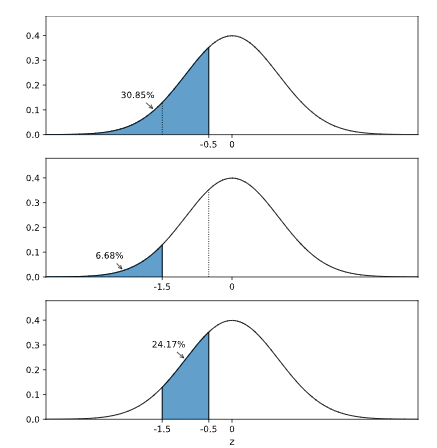
- The probability of a z-value smaller than -0.5 (shorter than 165 cm) is 30.85%
- The probability of a z-value smaller than -1.5 (shorter than 155 cm) is 6.68%
Subtract 6.68% from 30.85% to find the probability of getting a z-value between them.
30.85% - 6.68% = 24.17%
Here is a set of graphs illustrating the process:
Finding the Z-value of a P-Value
You can also use p-values (probability) to find z-values.
For example:
The p-value is 0.9, or 90%.
Using a Z-table or programming we can calculate the z-value:
Example
With Python use the Scipy Stats library norm.ppf() function find the z-value separating the top 10% from the bottom 90%:
import scipy.stats as stats
print(stats.norm.ppf(0.9))
Example
With R use the built-in qnorm() function find the z-value separating the top 10% from the bottom 90%:
qnorm(0.9)
