Learn Statistics Hypothesis Testing a Mean
Hypothesis testing for a mean involves determining whether a sample mean is significantly different from a hypothesized population mean. Here’s a detailed guide for hypothesis testing a mean:
Hypothesis Testing a Mean
The following steps are used for a hypothesis test:
- Check the conditions
- Define the claims
- Decide the significance level
- Calculate the test statistic
- Conclusion
For example:
- Population: Nobel Prize winners
- Category: Age when they received the prize.
And we want to check the claim:
"The average age of Nobel Prize winners when they received the prize is more than 55"
By taking a sample of 30 randomly selected Nobel Prize winners we could find that:

From this sample data we check the claim with the steps below.
Checking the Conditions
The conditions for calculating a confidence interval for a proportion are:
- The sample is randomly selected
- And either:
- The population data is normally distributed
- Sample size is large enough
A moderately large sample size, like 30, is typically large enough.
In the example, the sample size was 30 and it was randomly selected, so the conditions are fulfilled.
Note: Checking if the data is normally distributed can be done with specialized statistical tests.
Defining the Claims

This is a 'right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.
If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.
Deciding the Significance Level
The significance level (α) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.
The significance level is a percentage probability of accidentally making the wrong conclusion.
Typical significance levels are:
- α = 0.1 (10%)
- α = 0.05 (5%)
- α = 0.01 (1%)
A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.
There is no "correct" significance level - it only states the uncertainty of the conclusion.
Note: A 5% significance level means that when we reject a null hypothesis:
We expect to reject a true null hypothesis 5 out of 100 times.
Calculating the Test Statistic
The test statistic is used to decide the outcome of the hypothesis test.
The test statistic is a standardized value calculated from the sample.
The formula for the test statistic (TS) of a population mean is:
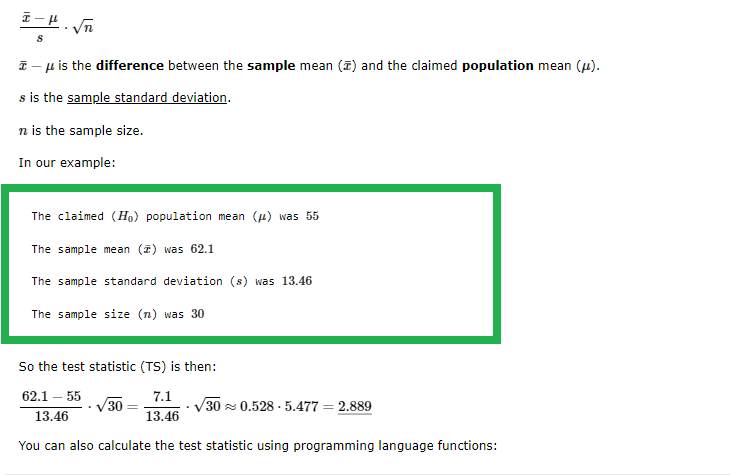
Example
With Python use the scipy and math libraries to calculate the test statistic.
import scipy.stats as stats
import math
# Specify the sample mean (x_bar), the sample standard deviation (s), the mean claimed in the null-hypothesis (mu_null), and the sample size (n)
x_bar = 62.1
s = 13.46
mu_null = 55
n = 30
# Calculate and print the test statistic
print((x_bar - mu_null)/(s/math.sqrt(n)))
Example
With R use built-in math and statistics functions to calculate the test statistic.
# Specify the sample mean (x_bar), the sample standard deviation (s), the mean claimed in the null-hypothesis (mu_null), and the sample size (n)
x_bar <- 62.1
s <- 13.46
mu_null <- 55
n <- 30
# Output the test statistic
(x_bar - mu_null)/(s/sqrt(n))
Concluding
There are two main approaches for making the conclusion of a hypothesis test:
- The critical value approach compares the test statistic with the critical value of the significance level.
- The P-value approach compares the P-value of the test statistic and with the significance level.
Note: The two approaches are only different in how they present the conclusion.
The Critical Value Approach
For the critical value approach we need to find the critical value (CV) of the significance level (α).
For a population mean test, the critical value (CV) is a T-value from a student's t-distribution.
This critical T-value (CV) defines the rejection region for the test.
The rejection region is an area of probability in the tails of the standard normal distribution.
Because the claim is that the population mean is more than 55, the rejection region is in the right tail:
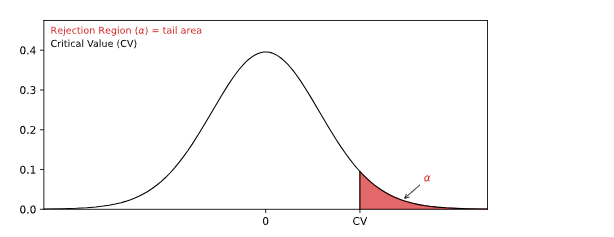
The size of the rejection region is decided by the significance level (α).
The student's t-distribution is adjusted for the uncertainty from smaller samples.
This adjustment is called degrees of freedom (df), which is the sample size (n)-1
In this case the degrees of freedom (df) is: 30-1=29
Choosing a significance level (α) of 0.01, or 1%, we can find the critical T-value from a T-table, or with a programming language function:
Example
With Python use the Scipy Stats library t.ppf() function find the T-Value for an = 0.01 at 29 degrees of freedom (df).
import scipy.stats as stats
print(stats.t.ppf(1-0.01, 29))
Example
With R use the built-in qt() function to find the t-value for an
α = 0.01 at 29 degrees of freedom (df).
qt(1-0.01, 29)
Using either method we can find that the critical T-Value is ≈ 2.462
For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).
If the test statistic is bigger than the critical value, the test statistic is in the rejection region.
When the test statistic is in the rejection region, we reject the null hypothesis (Ho).
Here, the test statistic (TS) was ≈ 2.889 and the critical value was ≈ 2.462
Here is an illustration of this test in a graph:
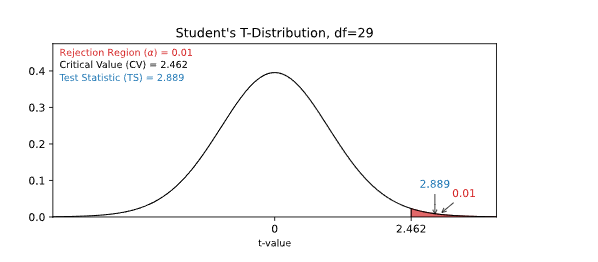
Since the test statistic was bigger than the critical value we reject the null hypothesis.
This means that the sample data supports the alternative hypothesis.
And we can summarize the conclusion stating:
The sample data supports the claim that "The average age of Nobel Prize winners when they received the prize is more than 55" at a 1% significance level.
The P-Value Approach
For the P-value approach we need to find the P-value of the test statistic (TS).
If the P-value is smaller than the significance level (α), we reject the null hypothesis (Ho).
The test statistic was found to be ≈ 2.889
For a population proportion test, the test statistic is a T-Value from a student's t-distribution.
Because this is a right tailed test, we need to find the P-value of a t-value bigger than 2.889.
The student's t-distribution is adjusted according to degrees of freedom (df), which is the sample size (30) - 29
We can find the P-value using a T-table, or with a programming language function:
Example
With Python use the Scipy Stats library t.cdf() function find the P-value of a T-value bigger than 2.889 at 29 degrees of freedom (df):
import scipy.stats as stats
print(1-stats.t.cdf(2.889, 29))
Example
With R use the built-in pt() function find the P-value of a T-Value bigger than 2.889 at 29 degrees of freedom (df):
1-pt(2.889, 29)
Calculating a P-Value for a Hypothesis Test with Programming
Many programming languages can calculate the P-value to decide outcome of a hypothesis test.
Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.
The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.
Example
With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a mean.
Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean bigger than 55.
import scipy.stats as stats
import math
# Specify the sample mean (x_bar), the sample standard deviation (s), the mean claimed in the null-hypothesis (mu_null), and the sample size (n)
x_bar = 62.1
s = 13.46
mu_null = 55
n = 30
# Calculate the test statistic
test_stat = (x_bar - mu_null)/(s/math.sqrt(n))
# Output the p-value of the test statistic (right tailed test)
print(1-stats.t.cdf(test_stat, n-1))
Example
With R use built-in math and statistics functions find the P-value for a right tailed hypothesis test for a mean.
Here, the sample size is 30, the sample mean is 62.1, the sample standard deviation is 13.46, and the test is for a mean bigger than 55.
# Specify the sample mean (x_bar), the sample standard deviation (s), the mean claimed in the null-hypothesis (mu_null), and the sample size (n)
x_bar <- 62.1
s <- 13.46
mu_null <- 55
n <- 30
# Calculate the test statistic
test_stat = (x_bar - mu_null)/(s/sqrt(n))
# P-value the p-value of the test statistic (right tailed test)
1-pt(test_stat, n-1)