Learn Statistics Standard Deviation
Standard deviation is the most commonly used measure of variation, which describes how spread out the data is.
Standard Deviation
Standard deviation (σ) measures how far a 'typical' observation is from the average of the data (μ).
Standard deviation is important for many statistical methods.
Here is a histogram of the age of all 934 Nobel Prize winners up to the year 2020, showing standard deviations:
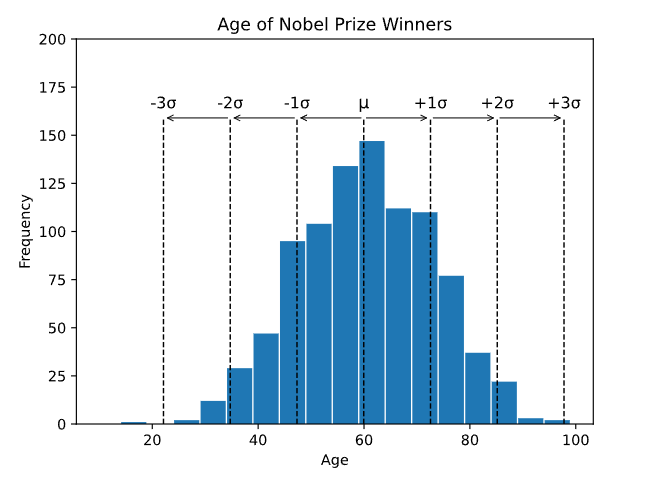
Each dotted line in the histogram shows a shift of one extra standard deviation.
If the data is normally distributed:
- Roughly 68.3% of the data is within 1 standard deviation of the average (from μ-1σ to μ+1σ)
- Roughly 95.5% of the data is within 2 standard deviations of the average (from μ-2σ to μ+2σ)
- Roughly 99.7% of the data is within 3 standard deviations of the average (from μ-3σ to μ+3σ)
Note: A normal distribution has a "bell" shape and spreads out equally on both sides.


Calculating the Standard Deviation with Programming
The standard deviation can easily be calculated with many programming languages.
Using software and programming to calculate statistics is more common for bigger sets of data, as calculating by hand becomes difficult.
Population Standard Deviation
Example
With Python use the NumPy library std() method to find the standard deviation of the values 4,11,7,14:
import numpy
values = [4,11,7,14]
x = numpy.std(values)
print(x)
Example
Use an R formula to find the standard deviation of the values 4,11,7,14:
values <- c(4,7,11,14)
sqrt(mean((values-mean(values))^2))
Sample Standard Deviation
Example
With Python use the NumPy library std() method to find the sample standard deviation of the values 4,11,7,14:
import numpy
values = [4,11,7,14]
x = numpy.std(values, ddof=1)
print(x)
Example
Use the R sd() function to find the sample standard deviation of the values 4,11,7,14:
values <- c(4,7,11,14)
sd(values)
Statistics Symbol Reference
