Learn Statistics Hypothesis Testing

---

Hypothesis testing is a formal way of checking if a hypothesis about a population is true or not.

---

Hypothesis TestingHypothesis Testing

Hypothesis testing is a statistical method used to make decisions about a population parameter based on a sample. It involves the following steps:

1. Formulate Hypotheses:



• Null Hypothesis (H₀): Assumes no effect or no difference.
• Alternative Hypothesis (H₁ or Ha): Assumes some effect or difference.



2. Choose a Significance Level (α):



• Common values are 0.05, 0.01, or 0.10.
• It represents the probability of rejecting the null hypothesis when it is actually true (Type I error).



3. Select the Appropriate Test:



• Depending on the data and hypotheses, choose a test (e.g., t-test, chi-square test).



4. Calculate the Test Statistic:



• Use the sample data to calculate a statistic that will be compared to a critical value.



5. Determine the p-value:



• The p-value indicates the probability of observing the test results under the null hypothesis.



6. Compare p-value with α:



• If p-value ≤ α, reject H₀ (evidence supports H₁). If p-value > α, do not reject H₀ (not enough evidence to support H₁).



7. Draw a Conclusion:



• Based on the comparison, conclude whether or not there is enough evidence to support the alternative hypothesis.

---

The Test Statistic

The test statistic is used to decide the outcome of the hypothesis test.

The test statistic is a standardized value calculated from the sample.

Standardization means converting a statistic to a well known probability distribution.

The type of probability distribution depends on the type of test.

Common examples are:

Note: You will learn how to calculate the test statistic for each type of test in the following chapters.

---

The Critical Value and P-Value Approach

There are two main approaches used for hypothesis tests:

• The critical value approach compares the test statistic with the critical value of the significance level.
• The p-value approach compares the p-value of the test statistic and with the significance level.

The Critical Value Approach

The critical value approach checks if the test statistic is in the rejection region.

The rejection region is an area of probability in the tails of the distribution.

The size of the rejection region is decided by the significance level ().

The value that separates the rejection region from the rest is called the critical value.

Here is a graphical illustration:

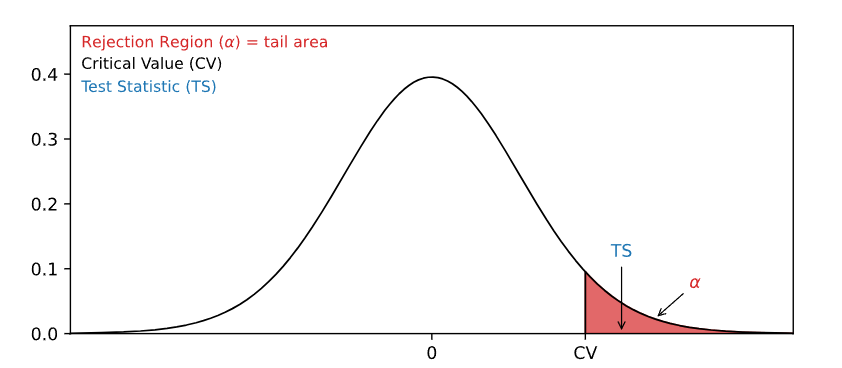
If the test statistic is inside this rejection region, the null hypothesis is rejected. For example, if the test statistic is 2.3 and the critical value is 2 for a significance level (α=0.05):

The P-Value Approach

The p-value approach checks if the p-value of the test statistic is smaller than the significance level ().

The p-value of the test statistic is the area of probability in the tails of the distribution from the value of the test statistic.

Here is a graphical illustration:

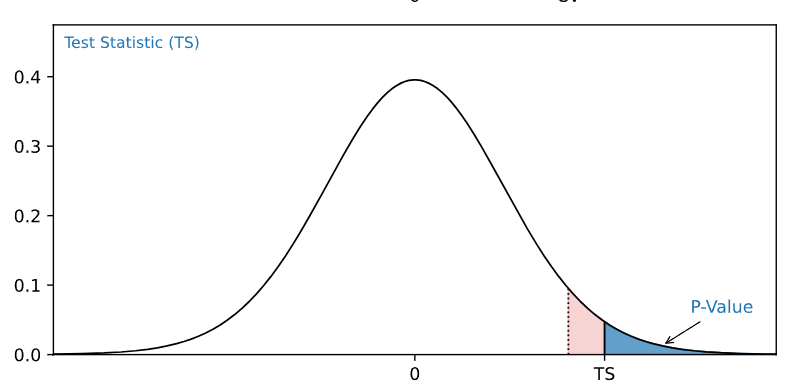
If the p-value is smaller than the significance level, the null hypothesis is rejected.

The p-value directly tells us the lowest significance level where we can reject the null hypothesis.

For example, if the p-value is 0.03:

Note: The two approaches are only different in how they present the conclusion.

---

Steps for a Hypothesis Test

The following steps are used for a hypothesis test:

1. Check the conditions
2. Define the claims
3. Decide the significance level
4. Calculate the test statistic
5. Conclusion

One condition is that the sample is randomly selected from the population.

The other conditions depends on what type of parameter you are testing the hypothesis for.

Common parameters to test hypotheses are:

• Proportions (for qualitative data)
• Mean values (for numerical data)

You will learn the steps for both types in the following pages.

Next